1. Tujuan [kembali]
- Untuk mengetahui dasar teori dari rangkaian Adder dan Substractor
- Mengetahui dan memahami cara kerja Adder dan Substractor
2. Alat dan Bahan [kembali]
3. Dasar Teori [kembali]

Tabel kebenaran untuk fungsi XOR diberikan pada tabel 1, dari tabel tersebut terlihat bahwa tabel tersebut sama seperti tabel kebenaran gerbang OR, kecuali bila semua masukan adalah tinggi (1), gerbang XOR akan membangkitkan keluaran rendah (0).
Gerbang XOR hanya akan terbuka bila muncul satuan bilangan ganjil pada masukan. Baris 2 dan 3 dari tabel kebenaran mempunyai satuan bilangan ganjil, oleh karena itu keluaran akan terbuka dengan level logika tinggi (1). Baris 1 dan 4 dari tabel kebenaran tersebut berisi satuan bilangan genap (0 dan 2), oleh karena itu gerbang XOR tidak terbuka dan akan muncul logika rendah (0) pada keluaran.
Binary Addition Circuits
Penambahan dan Pengurangan adalah dua Operasi Aritmatika dasar yang harus dilakukan oleh Komputer Digital mana pun. Jika kedua operasi ini dapat diterapkan dengan benar, maka tugas Perkalian dan Pembagian menjadi mudah (karena perkalian adalah penjumlahan berulang dan pembagian adalah pengurangan berulang).
Pertimbangkan operasi penjumlahan dua bilangan biner, yang merupakan salah satu tugas mendasar yang dilakukan oleh komputer digital. Empat operasi penjumlahan dasar dua bilangan biner bit tunggal adalah:
- 0 + 0 = 0
- 1 + 0 = 1
- 0 + 1 = 1
- 1 + 1 = (Carry)1 0
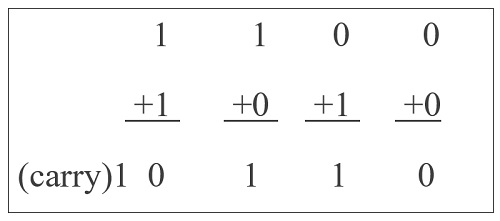
Dalam tiga operasi pertama, setiap penambahan biner memberikan jumlah sebagai satu bit, yaitu 0 atau 1. Tetapi untuk operasi penjumlahan keempat (di mana inputnya adalah 1 dan 1), hasilnya terdiri dari dua digit biner. Di sini, bit signifikan yang lebih rendah disebut sebagai 'Sum Bit', sedangkan bit signifikan yang lebih tinggi disebut sebagai 'Carry Bit'.
Untuk penambahan bit tunggal, mungkin tidak ada masalah. Masalah mungkin muncul ketika kita mencoba menjumlahkan bilangan biner dengan lebih dari satu bit.
Rangkaian logika yang dirancang untuk melakukan penjumlahan dua bilangan biner disebut sebagai Rangkaian Penambah Biner. Bergantung pada bagaimana mereka menangani output dari penambahan '1+1', mereka dibagi menjadi:
- Half Adder
- Full Adder
Let us take a look at the binary addition performed by various adder circuits.
Half Adder
Rangkaian logika yang digunakan untuk menjumlahkan dua angka 1-bit atau hanya dua bit disebut sebagai rangkaian Half Adder. Rangkaian ini memiliki dua input dan dua output. Inputnya adalah dua angka biner 1-bit (dikenal sebagai Augend dan Addend) dan outputnya adalah Sum dan Carry.
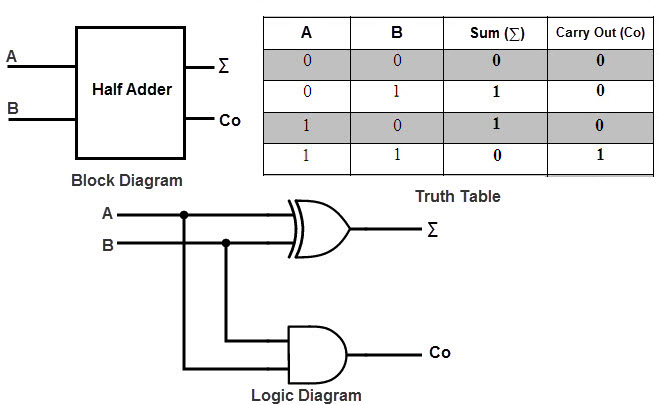
Gambar berikut menunjukkan diagram blok Half Adder.
Tabel kebenaran Half Adder ditunjukkan pada tabel berikut.
| INPUT | OUTPUT | ||
| A | B | Sum | Carry |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Jika kita mengamati nilai 'Jumlah' pada tabel kebenaran di atas, itu menyerupai Gerbang Ex-OR. Demikian pula, nilai 'Carry' pada tabel kebenaran di atas menyerupai Gerbang AND.
Jadi, untuk menerapkan Half Adder dengan benar, Anda memerlukan dua Gerbang Logika: gerbang XOR untuk Output 'Jumlah' dan gerbang AND untuk output 'Carry'. Gambar berikut menunjukkan Diagram Logika Half Adder.
Pada rangkaian setengah penambah di atas, input diberi label sebagai A dan B. Output 'Jumlah' diberi label sebagai simbol penjumlahan (∑) dan output Carry diberi label dengan CO.
Half adder terutama digunakan untuk penambahan augend dan addend dari bilangan biner orde pertama yaitu, bilangan biner 1-bit. Kami tidak dapat menambahkan bilangan biner dengan lebih dari satu bit karena Half Adder tidak dapat menyertakan informasi 'Carry' dari jumlah sebelumnya.
Karena keterbatasan ini, Half Adder praktis tidak digunakan di banyak aplikasi, terutama dalam penjumlahan multi-digit. Dalam aplikasi tersebut, carry dari penambahan digit sebelumnya harus ditambahkan bersama dengan dua bit; maka itu adalah tambahan tiga bit.
Full Adder
Full Adder adalah rangkaian logika kombinasional yang melakukan penjumlahan pada tiga bit dan menghasilkan dua output: Sum dan Carry. Seperti yang telah kita lihat bahwa Half Adder tidak dapat merespons tiga input dan karenanya full adder digunakan untuk menjumlahkan tiga digit sekaligus.
Terdiri dari tiga input, dua di antaranya adalah variabel input yang mewakili dua bit signifikan yang akan ditambahkan, sedangkan terminal input ketiga adalah carry dari penambahan sebelumnya. Kedua output tersebut adalah output Sum dan Carry.
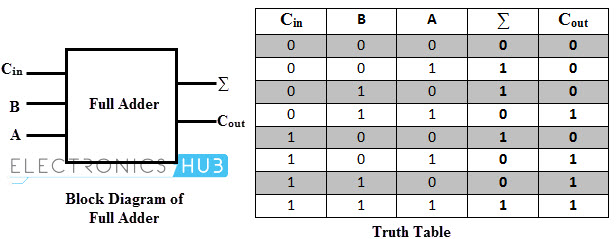
Gambar berikut menunjukkan diagram blok dari Full Adder di mana input diberi label sebagai A, B dan CIN, sedangkan output diberi label sebagai dan COUT.
Coming to the truth table, the following table shows the truth table of a Full Adder.
| INPUT | OUTPUT | |||
| A | B | CIN | Sum | COUT |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Dari tabel kebenaran di atas, kita dapat memperoleh Ekspresi Boolean untuk Output Sum dan Carry. Dengan menggunakan ekspresi tersebut, kita dapat membangun rangkaian logika untuk Full Adder. Tetapi dengan menyederhanakan persamaan lebih lanjut, kita dapat memperoleh titik di mana Penambah Penuh dapat dengan mudah diimplementasikan menggunakan dua Penambah Setengah dan Gerbang OR.
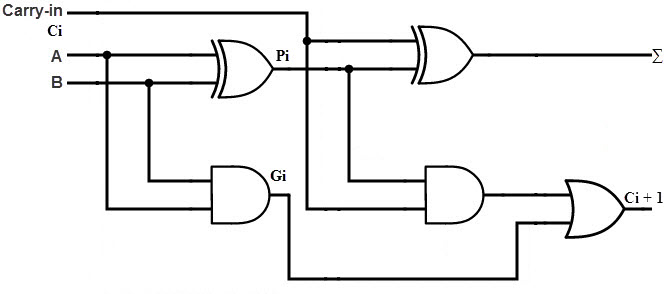
Gambar berikut menunjukkan Sirkuit Penambah Penuh yang diimplementasikan menggunakan dua Penambah Setengah dan Gerbang OR. Di sini, A dan B adalah bit input utama, CIN adalah input carry, dan COUT masing-masing adalah Output Sum dan Carry.
Parallel Binary Adders
Seperti yang telah kita diskusikan, satu Full Adder melakukan penambahan dua angka satu bit dan juga input carry. Untuk melakukan penjumlahan bilangan biner dengan lebih dari satu bit, diperlukan lebih dari satu penambah penuh dan jumlah Penambah Penuh tergantung pada jumlah bit. Jadi, Parallel Adder, adalah kombinasi dari Multiple Full Adders dan digunakan untuk menjumlahkan semua bit dari dua angka secara bersamaan.
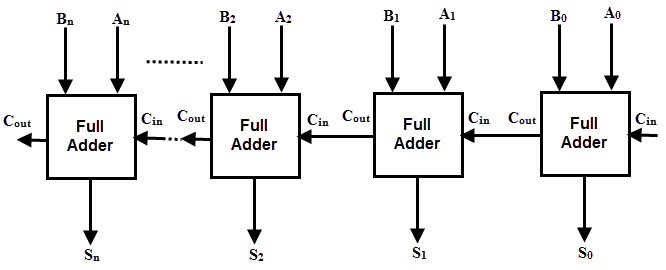
Dengan menghubungkan 'n' jumlah penambah penuh secara paralel, Penambah Paralel n-bit dapat dibangun. Dari gambar di bawah ini, perlu dicatat bahwa tidak ada carry pada posisi paling tidak signifikan, oleh karena itu kita dapat menggunakan half adder atau membuat input carry dari full adder sebagai nol pada posisi ini.
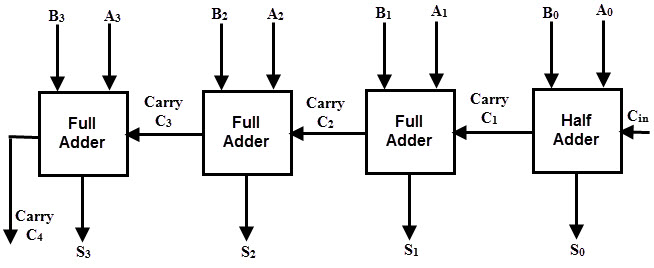
Gambar berikut menunjukkan Parallel 4-bit Binary Adder, yang memiliki tiga full adder dan satu half adder. Dua bilangan biner yang akan ditambahkan adalah 'A3 A2 A1 A0' dan 'B3 B2 B1 B0' , yang diterapkan ke input yang sesuai dari Penambah Penuh. Penambah paralel ini menghasilkan hasil mereka sebagai 'C4 S3 S2 S1 S0' , di mana C4 adalah carry terakhir.Dalam penambah 4 bit, blok pertama adalah penambah setengah yang memiliki dua input sebagai A0 B0 dan menghasilkan jumlah S0 dan bit pembawa C1. Blok pertama juga bisa menjadi full adder dan jika ya, maka input Carry C0 harus 0.
Tiga blok berikutnya harus merupakan penambah penuh, karena ada tiga input yang diterapkan padanya (dua bit biner utama dan bit Carry dari tahap sebelumnya).
Oleh karena itu, penambah penuh blok kedua menghasilkan jumlah S1 dan carry C2. Ini akan diikuti oleh dua penambah penuh lainnya dan dengan demikian hasil akhirnya adalah C4 S3 S2 S1 S0.
Umumnya, Penambah Penuh dirancang dalam sirkuit terpadu paket in-line ganda. 74LS283 adalah IC penambah penuh 4-bit yang populer. Unit Aritmatika dan Logika atau ALU dari sebuah unit komputer terdiri dari penjumlah paralel ini untuk melakukan penjumlahan bilangan biner.
Binary Subtraction Circuits
Operasi aritmatika dasar lain yang harus dilakukan oleh Komputer Digital adalah Pengurangan. Pengurangan adalah operasi matematika di mana satu bilangan bulat dikurangi dari yang lain untuk mendapatkan jumlah yang setara. Angka dari mana angka lain akan dikurangkan disebut sebagai 'Minuend' dan angka yang dikurangi dari minuend disebut 'Subtrahend'.
Mirip dengan penjumlahan biner, pengurangan biner juga memiliki empat kemungkinan operasi dasar. Mereka:
- 0 – 0 = 0
- 0 – 1 = (Borrow)1 1
- 1 – 0 = 1
- 1 – 1 = 0
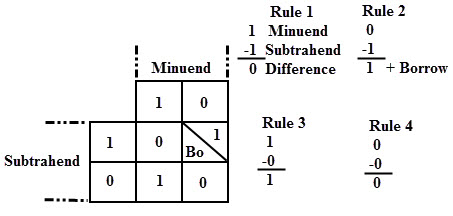
Gambar di atas menunjukkan empat kemungkinan aturan atau operasi dasar dari pengurangan biner. Dalam semua operasi, setiap bit subtrahend dikurangkan dari bit minuend.
Tetapi pada aturan kedua, bit minuend lebih kecil dari bit pengurangan, maka 1 dipinjam untuk melakukan pengurangan. Mirip dengan rangkaian penambah, rangkaian pengurangan dasar juga terdiri dari dua jenis:
- Half Subtractor
- Full Subtractor
Half Subtractors
Half Subtractor adalah Rangkaian Logika Kombinasional keluaran ganda yang melakukan pengurangan dua bilangan biner 1-bit. Ini memiliki dua input dan dua output. Kedua input sesuai dengan dua angka biner 1-bit dan dua output sesuai dengan bit Difference dan Borrow bit (berbeda dengan Sum dan Carry di Half Adder).
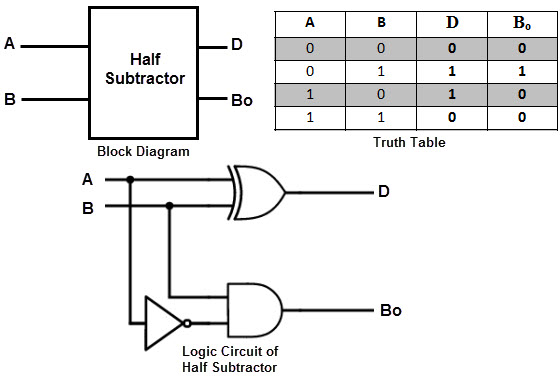
Gambar berikut menunjukkan diagram blok dari Half Subtractor.
Gambar
Tabel berikut menunjukkan tabel kebenaran Pengurang Setengah.
| INPUT | OUTPUT | ||
| A | B | Difference | Borrow |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
Dari tabel kebenaran di atas, kita dapat mengatakan bahwa output 'Difference' dari Half Subtractor mirip dengan output XOR (yang juga sama dengan output Sum dari Half Adder). Dengan demikian, Pengurangan Setengah juga dilakukan oleh gerbang Ex-OR dengan gerbang AND dengan satu input terbalik dan satu input normal, yang memerlukan operasi Borrow.
Gambar berikut menunjukkan rangkaian logika Half Adder.
Sirkuit ini mirip dengan Half Adder dengan hanya perbedaan menjadi input minuend yaitu, A dilengkapi sebelum diterapkan pada gerbang AND untuk mengimplementasikan output pinjaman.
Dalam kasus pengurangan multi-digit, pengurangan antara dua digit harus dilakukan bersama dengan peminjaman dari pengurangan digit sebelumnya, dan karenanya seorang pengurang harus memiliki tiga input, yang tidak mungkin dilakukan dengan Pengurang Setengah. Oleh karena itu, setengah subtraktor memiliki rangkaian aplikasi yang terbatas dan secara tegas, itu tidak digunakan dalam praktik.
Rangkaian logika yang digunakan untuk melakukan operasi pengurangan bilangan biner1 bit adalah ...
A. FULL SUBTRACTOR
B. HALF SUBTRACTOR
C. FULL ADDER
D. HALF ADDER
Rangkaian logika yang digunakan untuk melakukan operasi pengurangan bilangan biner 1 bit adalah ...
a. SUM
b. BORROW
c. CARRY OUT
d. DIFFERENCE







Tidak ada komentar:
Posting Komentar